О повышении информативности теста тонометрии

Авторы

• Любимов Г.А., доктор физико-математических наук, главный научный сотрудник;
• Моисеева И.Н., кандидат физико-математических наук, старший научный сотрудник;
• Штейн А.А., кандидат физико-математических наук, ведущий научный сотрудник.

Московский государственный университет им. М.В. Ломоносова, Научно-исследовательский институт механики, лаборатория общей гидромеханики

Тест тонометрии используется в офтальмологии для оценки внутриглазного давления (ВГД). Этот тест был введен в медицинскую практику русским врачом А.Н. Маклаковым в конце ХIХ века [1]. Приборная реализация теста заключается в том, что измеряется какой-либо геометрический параметр b, характеризующий деформацию оболочки глазного яблока (обычно роговицы) при том или ином внешнем нагружении: грузом различной величины с помощью механических нагружающих устройств — тонометров (плоских, выпуклых, вогнутых) или струей воздуха.

Предполагается или устанавливается в результате дополнительных опытов или модельных соображений, что измеренная величина в основном зависит только от давления p0 в глазу до начала опыта («истинного» давления) и практически не зависит от других механических характеристик оболочки глаза: ее формы, строения, упругих свойств и т. д.

Таким образом, принимается эмпирическая связь

b=b(p0) (1),

которая в таком виде (а чаще в виде таблицы или номограммы) используется для оценки величины p0 по измеренному значению параметра b.

В частности, в устройстве, предложенном Маклаковым [1, 2], используется для нагружения роговицы глаза тонометр с плоской контактной поверхностью и измеряется диаметр d площади контакта груза с роговицей после нагружения. При этом, как показывают экспериментальные исследования на выделенных глазах [3], ВГД в нагруженном глазу pt (тонометрическое давление) связано с d и весом тонометра G простой формулой Ингбера – Фика, соответствующей пренебрежению сопротивлением роговицы изгибу (2).

В результате многочисленных опытов на выделенных глазах и богатейшей медицинской практики были установлены эмпирические связи (3), которые, представленные в виде таблицы , используются для оценки истинного давления при измерении методом Маклакова [2].

Очевидно, что вид функции (1) определяется, в первую очередь, способом воздействия на глаз и измеряемым параметром b, но также и процедурой обоснования этого соотношения, на практике всегда приближенного. Различие в значениях величины p0, измеренной разными методами тонометрии (разная форма груза при нагружении глаза, характеристики воздушного воздействия на глаз и т. д.) на одном и том же глазу, зависит от сравниваемых методов, точности измерения величины b и соответствия предположений, принятых при обосновании соотношения (1), реальной картине физических процессов в глазу в условиях данного метода измерения. То, что такое различие (порядка 3-4 мм рт. ст.) в величинах p0, измеренных разными методами, может существовать, известно практическим врачам.

Существует еще один вопрос, связанный с точностью измерения p0 любым из существующих методов тонометрии. Эмпирические связи типа (1), (3) устанавливаются обычно на основе статистической обработки данных измерений на группе здоровых испытуемых. После того как эти соотношения обоснованы и тем самым обоснован метод измерения, он применяется во всех случаях. При этом вопрос о точности измерения и влиянии индивидуальных особенностей испытуемых на измеряемую величину p0, как правило, не ставится. Тем не менее хорошо известно, что форма глазного яблока, например, у больных миопией, заметно отличается от формы здорового глаза. Существенные индивидуальные различия, даже в группе здоровых испытуемых, имеют значения параметров, характеризующих упругие свойства оболочки глаза [4]. Очевидно, что все эти факторы могут влиять на деформацию оболочки конкретного глаза при том или ином способе его нагружения, и, следовательно, на результат измерений.

В работе [5] на основе математической модели глаза, обоснованной в [6] и максимально просто отражающей его основные механические свойства, численно исследовано влияние формы контактной поверхности тонометра, который используется при тонометрии, и параметров, характеризующих упругие свойства оболочки глаза, на измеряемую при тонометрии величину ВГД. При этом упругие свойства модельной оболочки описывались двумя параметрами: Ec, характеризующим жесткость роговицы, и Es, характеризующим жесткость склерального сегмента оболочки и окружающих его тканей. Показано, что небольшая модификация метода тонометрии позволяет не только уточнить ее результаты для конкретного испытуемого, но и оценить индивидуальные значения упругих констант, которые могут иметь самостоятельный диагностический интерес.

Результаты расчетов [5] позволяют сделать некоторые выводы относительно возможностей метода тонометрии. Обсуждению этих выводов посвящена данная работа.

Определение внутриглазного давления

Для дальнейшего обсуждения выберем два типа тонометра с широким плоским основанием (тонометр Маклакова) и с широким выпуклым основанием (конвекс-тонометр Краснова [7]). В обоих случаях в качестве измеряемой величины выбран радиус области контакта роговицы глаза с грузом r*.

(а) Определение тонометрического давления pt

Расчеты показывают, что для принятой в [5, 6] модели глазного яблока величина r* в основном определяется величиной тонометрического давления pt (внутриглазного давления в глазу, нагруженном тонометром определенной формы и веса).

Для тонометра с плоским основанием имеет место точное (в рамках модели) соотношение (2), из которого непосредственно видно, что связь r*= r*(pt) зависит в этом случае только от веса тонометра G и не зависит от жесткости оболочки глазного яблока.

На рис. 1 (кривая 1) представлена кривая, рассчитанная по формуле (2), для этого тонометра при весе груза 10 г.

Анализ кривой показывает, что измерение радиуса области контакта с точностью порядка 0,1 мм обеспечивает точность измерения тонометрического давления порядка 2 мм рт.ст. при низких значениях давления (точки А и В) и порядка 5 мм рт.ст. — при высоких (точки C и D).

Из расчета по модели [5, 6] для тонометра выпуклым основанием следует, что величина r* зависит не только от pt, но и от параметра Ec, характеризующего жесткость роговицы. Для примера на рис. 1 (кривая 2) приведена эта зависимость, соответствующая среднему значению этого параметра. Здесь и далее используются оценки средних значений упругих констант (Ec=0,3 МПа, Es=10 МПа), полученные на основе анализа эмпирического материала ([4, 8]) в [6]. Видно, что порядок точности измерения такой же, как для тонометра с плоским основанием.

Как показывает расчет [5], зависимость размера области контакта от жесткости роговицы слабая в широком диапазоне изменения Ec (0,2≤Ec≤1,2): разница давлений при заданном не превосходит величину 2-3 мм рт.ст., причем при том же весе G с ростом жесткости роговицы Ec радиус области контакта возрастает.

Зависимость, приведенная на рис. 1 для конвекс-тонометра, может использоваться при измерении тонометрического давления во всем диапазоне давлений, если жесткость роговицы испытуемого не слишком сильно отличается от ее среднего значения. При этом следует учитывать вышеупомянутые оценки для точности измерения. Очевидно, что показанные на рис. 1 зависимости могут быть представлены в виде таблиц и введены в компьютерное обеспечение метода.

При обработке результатов тонометрии у испытуемых с большим отличием жесткости роговицы от среднего значения для уточнения значений pt можно использовать индивидуальные расчетные кривые pt=pt(G,Ec). Эти кривые легко рассчитываются при известном индивидуальном значении параметра жесткости роговицы Ec, которое может быть оценено методом дифференциальной тонометрии (см. ниже).

Сложнее обстоит дело с обеспечением точности измерения размера области контакта r*, которая, как видно из предыдущего, сильно влияет на точность результата. В настоящее время точность измерения этой величины стандартными методами (включая эмпирическую поправку на ширину слоя слезы вокруг пятна контакта) не оценивается на числовом уровне, поэтому говорить о точности измерения тонометрического давления методами Маклакова и Краснова не представляется возможным.

Однако современное развитие оптических методов (например, оптическое обеспечение метода измерения внутриглазного давления по Гольдману [2]) позволяет в принципе решить задачу высокоточного определения площади контакта. И для метода Маклакова известен способ определения тонометрического давления с использованием прозрачного тонометра, на торцевую гладко отполированную аппланационную поверхность которого нанесены концентрические круги, соответствующие номограммам Маклакова – Поляка [9]. Этот метод при соответствующей технической и приборной реализации мог бы повысить точность определения тонометрического давления тонометрами Маклакова и Краснова. Возможно, для оценки диаметра пятна контакта на выпуклом тонометре окажется перспективным и оптический метод, кратко описанный в [7].

                

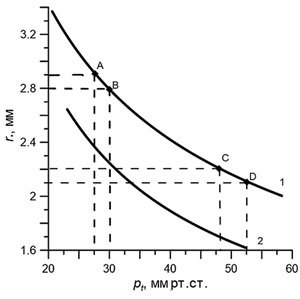
Рис. 1. Зависимость радиуса пятна контакта r* для тонометра с плоским (кривая 1) и выпуклым (2) основанием от тонометрического давления для веса тонометра 10 г

(б) Определение истинного внутриглазного давления p0 стандартным методом тонометрии

Из общих соображений физического характера следует, что, хотя для тонометра с плоским основанием связь между тонометрическим давлением pt и размером пятна контакта и роговицы r* не зависит от упругих свойств оболочки глазного яблока — параметров Ec и Es, сами величины pt и r* зависят от этих параметров и истинного ВГД p0 (внутриглазного давления до нагружения глаза тонометром), т. е., вообще говоря, существует связь r*= r*(p0, Ec, Es, G). Расчеты по модели [5, 6] показали, что увеличение жесткости роговицы Ec и склеральной области Es приводит при фиксированном p0 к уменьшению размера пятна контакта r*.

На рис. 2 в качестве примера приведены расчетные зависимости для тонометра с плоским основанием, соответствующие различным значениям склеральной жесткости для наиболее употребительного веса груза 10 г. Видно, что в этом диапазоне жесткостей разница в значениях p0, соответствующих заданному значению радиуса пятна контакта r*, составляет величину порядка 4-5 мм рт.ст. (заметим, что для тонометра весом 5 г эта величина будет порядка 1,5-2 мм рт.ст.). Кроме того, точность измерения величины r* порядка 0,1 мм приводит к точности измерения p0 порядка 3 мм рт.ст. для тонометра весом 10 г (для тонометра весом 5 г — порядка 1 мм рт.ст.). Что касается жесткости роговицы, то при варьировании Ec от 0,3 до 0,6 МПа значения p0 различаются не более чем на 1-2 мм рт.ст.

Для сравнения на рис. 2 приведена пунктирная кривая, которая соответствует зависимости, рекомендуемой в [2] для оценки p0 по радиусу пятна контакта при измерении истинного ВГД методом Маклакова (плоская поверхность контакта). Заметим, что в таблицах, приведенных в [2], p0 связывается с диаметром размытого из-за слезы отпечатка (большим чем d=2 r*), но для кривой, приведенной на рис. 2, проведен пересчет в соответствии с данными [2, 3] именно к r* — радиусу контакта тонометра с роговицей.

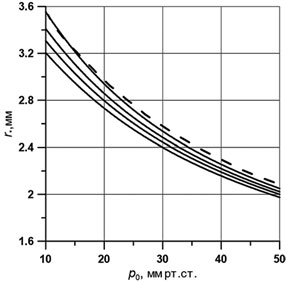
Рис. 2. Зависимость радиуса пятна контакта для тонометра с плоским основанием от истинного давления для среднего значения жесткости роговицы МПа при разных значениях жесткости склерального сегмента: снизу вверх (сплошные линии) 32, 16, 10, 6 МПа. Верхняя (пунктирная) кривая соответствует таблицам, приведенным в [2]

Из рис. 2 следует, что различие между зависимостями [2] и расчетными кривыми при заданном r* для средних значений жесткостей составляет величины порядка 2 мм рт.ст.

Форма пунктирной кривой на рис. 2 отражает результаты эмпирических исследований по уточнению метода Маклакова. Аналогичные сплошные кривые выражают свойства обоснованной в [6] и используемой в настоящей работе модели глазного яблока для разных значений упругих констант. Близость расчетных кривых к эмпирической может служить лишним подтверждением тому, что принятая модель глазного яблока удовлетворительно описывает физические процессы, происходящие в здоровом глазу при его нагружении в процессе тонометрии.

Следует иметь в виду, что зависимости, приведенные в [2], рассматриваются как универсальные и не учитывают индивидуального разброса упругих характеристик. Некоторое различие между кривыми, соответствующими средним значениям упругих констант, по нашим расчетам и по данным [2] связано с использованием разных массивов экспериментальных данных. Видно, что при больших значениях упругих характеристик роговицы: 0,3 МПа — кривая (1), 0,6 МПа — (2), 0,9 МПа — (3) для одной и той же склеральной жесткости 10 Мпа значениях Es (а высокая жесткость склеры часто встречается у страдающих глаукомой [10]) отличие от истинного давления, определенного по таблицам Нестерова, составит от 3,5 до 6 мм рт.ст. от рассчитанного с учетом индивидуальных свойств глазного яблока. Это отличие тем больше, чем больше значение Es.

                

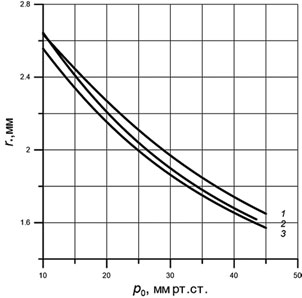
Рис. 3. Зависимость радиуса пятна контакта для тонометра весом 10 г с выпуклым основанием от истинного давления при разных значениях упругих констант: Ec=0,6 МПа, Es=10 МПа — кривая (1); Ec=0,3 МПа, Es=10 МПа — (2); Ec=0,3 МПа, Es=24 МПа — (3)

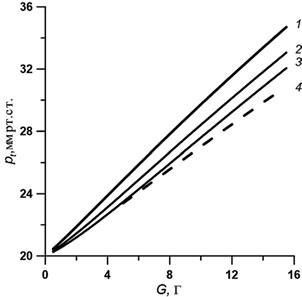
Рис. 4. Зависимость тонометрического давления от веса тонометра с плоским основанием при разных

Аналогичные рис. 2 расчетные кривые для выпуклого тонометра приведены на рис. 3. Сопоставление соответствующих кривых на рис. 2 и 3 убеждает в идентичности их качественного вида и зависимости от жесткостей склеры и роговицы. Отсюда следует, что точность измерения истинного ВГД p0 выпуклым и плоским тонометрами примерно одинакова.

Приведенные расчеты показывают, что точность определения истинного давления p0 рассматриваемыми тонометрами может быть существенно повышена. Одним из возможных путей в этом направлении может быть, как уже упоминалось, оптическая регистрация размера пятна контакта во время диагностической процедуры. Кроме того, точность измерения p0 будет повышена, если для каждого испытуемого будут в независимом исследовании оценены индивидуальные значения упругих констант Ec и Es (см. ниже). В этом случае для оценки нужно использовать индивидуальные кривые r*= r* (p0, Ec, Es, G). Поле индивидуальных кривых может быть построено по результатам работы [5] и введено в математическое обеспечение соответствующего прибора или затабулировано.

(в) Определение истинного внутриглазного давления методом дифференциальной тонометрии

Под дифференциальной тонометрией будем здесь понимать исследование, в котором одним и тем же тонометром измеряются два тонометрических давления pt1 и pt2, соответствующие различным грузам, последовательно приложенным к одному и тому же глазу. Таким образом, термин «дифференциальная тонометрия», хорошо отражающий суть процесса, здесь применяется расширительно (в медицинской литературе его традиционно используют для описанной процедуры, если она выполняется тонометром Шиотца). В случае тонометра Маклакова аналогичный метод был назван эластометрией [11], в настоящее время чаще говорят об эластотонометрии [8].

В работе [5] установлено, что для принятой механической модели глазного яблока и рассматриваемых форм тонометров зависимость pt=pt(G, p0 ,Ec,Es) в области весов 0≤G≤15 г практически линейна по G за исключением небольшой области малых значений G (рис. 4). Таким образом, сделав два тонометрических измерения тонометром выбранной формы с разными грузами G1 и G2, следуя процедуре, описанной в разд. 1а, можно по кривым, представленным на рис. 2, определить соответствующие им тонометрические давления pt1 и pt2, после чего вычисляется величина значениях Es: (1) — 6, (2) — 9, (3) — 12, (4) — 16 МПа 

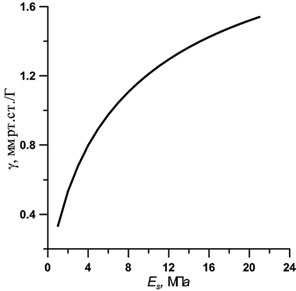
Рис. 5. Зависимость параметра от Es, рассчитанная для тонометра с выпуклым основанием при Ec=0,3 МПа

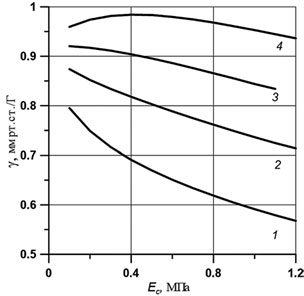
Рис. 6. Зависимость параметра от Ec, расчитанные для тонометра с плоским основанием при разных

В пренебрежении нелинейностью при малых G точка пересечения прямой pt=pt(G) с осью pt на плоскости pt,G соответствует величине истинного внутриглазного давления p0=pt(G=0). Следовательно, в принятом приближении из (4) величина p0 может быть вычислена через измеряемые величины pt1, pt2 и по формуле  (5).

Величина зависит, вообще говоря, от упругих свойств оболочки глаза, т. е. в рамках принятой в [5] модели глазного яблока от констант Ec и Es, характеризующих жесткость роговицы и склерального сегмента. Однако, как следует из расчетов [5] для выпуклого тонометра, величина практически не зависит от упругих свойств роговицы, т. е. = (Es). Для тонометра с плоским основанием величина зависит также и от жесткости роговицы (см. рис. 4).

Расчеты [5] показывают, что ошибка при определении p0 описанным в этом разделе способом, связанная с отличием истинной кривой pt=pt(G) на плоскости (pt,G) от прямой, составляет в реальном диапазоне параметров 1-2 мм рт.ст. Таким образом, этот способ может в принципе оказаться более точным, чем обычная тонометрия (разд. 1б). Программная реализация этого способа не представляет труда. Основные трудности здесь, как и в разд. 1б, связаны с необходимостью повышения точности измерения размера пятна контакта груза с роговицей глаза.

Оценка упругих характеристик оболочки глазного яблока на основе метода дифференциальной тонометрии

В описанных в разд. 1 методах возможной оценки тонометрического и истинного внутриглазного давлений использованы результаты численного решения модельной задачи о деформации оболочки глаза при ее нагружении тонометрами различной формы. При этом для получения численных результатов в ряде случаев использованы расчетные зависимости, соответствующие средним значениям параметров, характеризующих жесткости роговицы Ec и склерального сегмента Es (см. рис. 2-4). Если индивидуальные значения этих параметров для конкретного испытуемого существенно отличаются от средних, то точность оценки ВГД падает и становится неопределенной. Как уже указывалось, для уточнения оценки ВГД тем же методом измерения — тонометрией грузами различной формы — можно было бы воспользоваться численными решениями модельной задачи [5], если бы были известны индивидуальные значения параметров Ec и Es. Рассмотрим этот вопрос подробнее.

В разд. 1в было указано, что с помощью двух тонометрических измерений грузами разного веса можно оценить величину, которая при тонометрии выпуклым тонометром зависит практически только от параметра Es, характеризующего упругие свойства склерального сегмента = (Es). Расчетная зависимость, соответствующая среднему значению жесткости роговицы, представлена на рис. 5. Пользуясь этой кривой (или ее программной реализацией), при известной величине оценивается индивидуальное значение величины Es для данного испытуемого.

Для того, чтобы оценить индивидуальное значение величины Ec, характеризующей жесткость роговицы испытуемого глаза, необходимо выполнить дополнительно два тонометрических измерения тонометрами с плоским основанием разного веса [5]. Это измерение дает возможность определить параметр при измерении этим типом тонометра (каждой форме основания соответствует свое значение параметра). В разд. 1в уже говорилось, что этот параметр в данном случае зависит от обеих жесткостей Ec и Es: = (Es, Ec). Так как параметр для обследуемого глаза уже известен из измерений выпуклым штампом, то по расчетным кривым = (Es, Ec) (рис. 6) можно оценить значение параметра Ec.

Таким образом, в результате двух дифференциально-тонометрических измерений выпуклым и плоским грузами возможно оценить величины тонометрического и истинного внутриглазного давлений и индивидуальные значения параметров Ec и Es, характеризующих жесткость роговицы и склерального сегмента исследуемого глаза. Индивидуальные значения параметров Ec и Es могут служить для уточнения измеренных величин ВГД.

Вообще говоря, применив дифференциальную тонометрию тонометрами с разной формой основания и определив упругие характеристики Ec и Es, по любому из выполненных четырех измерений тонометрического давления возможно на основании рассматриваемой модели рассчитать истинное внутриглазное давление p0. Кроме того, давление p0 может быть оценено по формуле (5) (отдельно для каждого типа тонометра). Все эти значения могут не вполне совпадать как из-за неточности измерений, так и из-за грубости модели в сочетании с приближенным характером использованных методик их оценки. Сравнение нескольких таких оценок может быть использовано для уточнения значения истинного ВГД.

Упругие характеристики глазного яблока Ec и Es можно рассматривать как самостоятельные, имеющие отчетливый физиологический смысл, диагностические показатели. В частности, известно, что повышение склеральной жесткости коррелирует с вероятностью возникновения глаукомы [10]. Возможность неинвазивного определения параметров, отдельно отвечающих за упругие свойства роговицы и задней области глаза, отличает предлагаемую методику от оценки упругих свойств глазного яблока на основе данных о единственной упругой характеристике (по-разному определяемой «ригидности») [12]. Независимо от способа определения, такая единственная (по существу интегральная) характеристика не дает возможности раздельно оценить упругие свойства роговицы и склерального сегмента.

Заключение

В работе проанализированы свойства математической модели глазного яблока, обоснованной в [6], с целью оценки точности измерения тонометрического и истинного давлений методами тонометрии, использующими грузы постоянного веса с плоским (метод Маклакова) и выпуклым (метод конвекс-тонометрии) широкими основаниями и опирающимися на измерение радиуса (или диаметра) пятна контакта тонометра и роговицы. Показано, что точность измерения давлений этими методами относительно слабо зависит от веса и формы тонометра.

Основным техническим фактором, определяющим точность измерения, является точность определения размера пятна контакта тонометра и роговицы. Недостаточная точность измерения может, к примеру, сделать практически бесполезной максимально простую и удобную формулу (5). Упомянутые в разд.1а способы возможного повышения точности измерения пятна контакта при их технической реализации могут существенно повысить точность метода тонометрии.

Основным физиологическим фактором, исключающим оценку точности современных методов тонометрии, является отсутствие индивидуальных данных об упругих свойствах оболочки глаза испытуемого. Известно, что даже в группе здоровых испытуемых имеет место десятикратное изменение значений некоторых упругих характеристик [4]. В группе больных или лиц, перенесших оперативное вмешательство, эти изменения могут оказаться еще большими.

В данной работе на основе модельных расчетов показано (см. разд. 1), что изменение характеризующих упругость глазного яблока параметров даже в пределах их изменения для здоровых испытуемых может существенно влиять на измеряемую величину давления. Отсюда следует, что оценка жесткости оболочки глазного яблока имеет принципиальное значение для оценки точности тонометрии. Метод дифференциальной тонометрии грузами разной формы позволяет решить эту задачу. Использование предлагаемого метода позволяет оценить индивидуальные значения упругих характеристик роговицы и склеральной области Ecи Es, а также уточнить значение истинного ВГД.

Конечно, такая точная, но довольно сложная оценка ВГД необходима врачу далеко не всегда. Ясно, что массовое обследование здоровых испытуемых может проводиться, например, стандартным методом Маклакова. В тех же случаях, когда требуется большая точность, можно и нужно использовать усложненный и уточненный метод тонометрии двумя тонометрами, описанный в разд. 1, 2. В частности, уточнение может оказаться необходимым при сильном отклонении упругих свойств глазного яблока от средних значений.

Очевидно, что как всякий новый метод, этот метод нуждается в экспериментальной апробации. Авторы готовы сотрудничать с врачами-офтальмологами, которые проявят интерес к такой апробации.
В заключение еще раз обратим внимание на то, что возможность оценки на основе рассматриваемой модели глаза индивидуальных параметров жесткости глазного яблока раздельно для роговичного и склерального сегментов имеет и самостоятельное значение. Возможно, такая оценка даже более значима, чем уточнение величины истинного внутриглазного давления.

Литература / References

1. Маклаков А.Н. Офтальмотонометрия. Медицинское обозрение 1884; 24:1092-1095. [Maklaloff A.N. Ophthalmotonometry. Meditsinskoe obozrenie 1884; 24:1092-1095. (in Russ.)].
2. Нестеров А.П., Бунин Ф.Я., Кацнельсон Л.А. Внутриглазное давление. Физиология и патология. М.: Наука, 1974; 381 с. [Nesterov A.P., Bunin F.Ya., Katsnelson L.A. Vnutiglaznoe davlenie. Fiziologiya I patologiya [Intraocular Pressure: Physiology and Pathology] Moscow, Nauka Publ., 1974; 381 p. (in Russ.)].
3. Вургафт М.Б. О калибровке тонометров Маклакова разного веса. Офтальмологический журнал 1965; 6:443-448. [Vurgaft M.B. On the calibration of Maklakov’s tonometers of different weights. Oftalmologicheskii zhurnal 1965; 6:443-448. (in Russ.)].
4. Pallikaris I.G., Kymionis G.D., Ginis H.S., Kounis G.A., Tsilimbaris M.K. Ocular rigidity in living human eyes. Invest Ophthalmol Vis Sci 2005; 46(2):409-414. doi:10.1167/iovs.04-0162.
5. Любимов Г.А., Моисеева И.Н., Штейн А.А. Исследование свойств двухкомпонентной механической модели глазного яблока и возможности ее использования при практической оценке механических свойств глаза человека. Известия РАН. Механика жидкости и газа 2014; 6:5-16. [Lyubimov G.A., Moiseeva I.N., Stein A.A. Investigation of the properties of the two-component eyeball model and opportunities to use it for practically estimating the mechanical characteristics of the human eye. Fluid Dynamics 2014; 49(6):705-714.] doi:10.1134/ S0015462814060027.
6. Моисеева И.Н., Штейн А.А. Анализ зависимости давление – объем для глазного яблока, нагруженного плоским штампом, на основе двухсегментной упругой модели. Известия РАН. Механика жидкости и газа 2011; 5:3-15. [Moiseeva I.N., Stein A.A. Analysis of the pressure-volume relationship for the eyeball loaded by a flat stamp on the basis of a two-constant elastic model. Fluid Dynamics 2011; 46(5): 673-683. (in Russ.)]. doi:10.1134/S0015462811050012.
7. Краснов М.М. Новый принцип измерения ВГД (конвекс-тонометрия и конвекс-тонография). Вестник офтальмологии 1981; 1:53-54. [Krasnov M.M. A novel principle of measuring IOP (convex-tonometry and convex-tonography. Vestnik Oftalmologii 1981; 1:53-54. (in Russ.)].
8. Аветисов С.Э., Бубнова И.А., Антонов А.А. Диагностические возможности эластотонометрии. Глаукома: реальность и перспективы. М.: НИИ глазных болезней РАМН, 2008; Ч. 2:81-85. [Avetisov S.E., Bubnova I.A., Antonov A.A. Diagnostic opportunities of elastotonometry. Glaukoma: Realnost I perspectivy [Glaucoma: Reality and Promises] Moscow, State Research Institute of Eye Diseases of Russian Academy of Medical Sciences, 2008, Pt. 2: 81-85. (in Russ.)].
9. Ермолаев А.П., Першин Б.С., Антонов А.А. Тонометр для измерения внутриглазного давления в условиях операционной. Патент RU на полезное устройство № 91851. 2010. [Ermolaev A.P., Pershin B.S., Antonov A.A. Tonometer for measuring the intraocular pressure under the conditions of the Operating Room. Patent RU for a useful device No. 91851. 2010. (in Russ.)].
10. Иомдина Е.Н., Игнатьева Н.Ю., Данилов Н.А. Арутюнян Л.Л., Киселева О.А., Назаренко Л.А. Биохимические и cтруктурнобиомеханические особенности матрикса склеры человека при первичной открытоугольной глаукоме. Вестникофтальмологии 2011; 6:10-14. [Iomdina E.N., Ignatyeva N.Yu., Danilov N.A., Arutynyan L.L., Kiseleva O.A., Nazarenko L.A. Biochemical and structural-biomechanucal characteristics of human sclera matrix at primary open-angle glaucoma. Vestnik Oftalmologii 2011; 6:10-14. (in Russ.)].
11. Кальфа С.Ю. Эластометрия глаза. Русский офталмологический журнал 1928; 8:250-262. [Kalfa S.Yu. Elastometry of the eye. Russkii Oftalmologicheskii Zhurnal 1928; 8:250-262. (in Russ.)].
12. Штейн А.А. О понятии ригидности глаза. Российский общенациональный офтальмологический форум, 4-й. М., 2011; 2:257- 261. [Stein A.A. On the notion of eye rigidity. Russian National Ophthalmologic Forum, 4th. Moscow, Helmholtz Research Institute of Eye Diseases. 2011; 2:257-261. (in Russ.)].

http://www.glaucomajournal.ru/jour/article/view/85